Appunti di Architettura degli Elaboratori
Table of Contents
1. Rappresentazione dell'informazione
1.1. Proprietà delle codifiche
Per alfabeto A si intende un insieme finito e distinguibile di segni. Una parola o stringa su A è una sequenza finita di simboli di A. Indichiamo con A* tutte le possibili parole generabili dall'alfabeto A.
Un linguaggio L sull'alfabeto A è un qualsiasi sottoinsieme di A* (L ⊆ A*).
Associando gli elementi di un insieme D ad L otterremo una codifica di L. Una codifica è una funzione totale f: D → L:
- Se f non è suriettiva è ridondante: Se f è suriettiva ogni stringa in L è la codifica di almeno un elemento in D
- Se f non è iniettiva è ambigua: Se f è iniettiva ogni stringa in L corrisponde al più ad un solo elemento in D
- Una codifica è quindi non ambigua e non ridondante se è biunivoca
- ND è la cardinalità di D, mentre NL è la cardinalità di L:
- Se ND < NL allora qualsiasi codifica è ambigua
- Se NL < ND allora qualsiasi codifica è ridondante
Le proprietà delle codifiche sono quindi le seguenti:
- Ambiguità/Non ambiguità
- Ridondanza/Non Ridondanza
- Economicità (numero di simboli usati per unità di informazione)
- Semplicità nella codifica/decodifica
- Semplicità nell'operare sull'informazione codificata
1.2. Rappresentazione in una base generica
Ad ogni naturale b > 1 corrisponde una codifica in base b. L'alfabeto Ab consiste in b simboli che corrispondono ai numeri che vanno da 0 a b-1. Un numerale di cifre Ab rappresenta il numero: \[ \sum_{i=0}^{m-1}s \times b^i \]
Notazione standard:
- n denota un generico numero a prescindere dalla base
- nb denota un numero in base b, esempio: 10012 rappresenta il numero 9 (base dieci) in base 2.
1.2.1. Lunghezza e valore massimo rappresentabile
La lunghezza di n rispetto a b rappresenta il numero di cifre che occorrono per rappresentare quel numero nella data base:
- La lunghezza di 101 in base 2 è 7: 11001012
- In base 7: 2037
- In base 6: 2456
Il valore massimo rappresentabile in una base b con m cifre è dato dalla formula: \[ v_{max} = b^m - 1 \]
1.2.2. Cifre necessarie per rappresentare un numero
Per sapere quante cifre m occorrono per rappresentare un numero, il massimo numero rappresentabile con m dovrà essere maggiore o uguale allo stesso: \[ b^m - 1 \ge n \] \[ b^m \ge n + 1 \] \[ m \ge \log_b(n + 1) \]
1.2.3. Cambiamento di base
L'algoritmo di cambio di base consiste nel dividere ripetutamente n per la base di arrivo e di raccogliere i resti dalla cifra meno significativa a quella più significativa.
Per passare da una base diversa da quella decimale ad un'altra base ancora diversa, conviene dividere il problema in due parti:
- Convertire il numero in base 10
- Convertire il numero da base 10 alla base di arrivo
1.2.4. Esempio di conversione da base 5 a base 8
Supponiamo di voler convertire \(101_5\) in base 8:
- Primo, convertiamo \(101_5\) in base 10: \[ 101_5 = 1 \times 5^2 + 0 \times 5^1 + 1 \times 5^0 = 25 + 0 + 1 = 26_{10} \]
- Ora, convertiamo \(26_{10}\) in base 8: \[ 26 \div 8 = 3 \quad \text{con resto} \ 2 \] \[ 3 \div 8 = 0 \quad \text{con resto} \ 3 \] Quindi, raccogliamo i resti in ordine inverso e otteniamo: \[ 26_{10} = 32_8 \]
Pertanto, \(101_5 = 32_8\).
1.3. Codifica binaria e esadecimale
Possiamo usare dei trucchetti per rendere più semplice la codifica/decodifica in una base m potenza di 2, esempio:
- Poiché 16 = 24 è possibile utilizzare una cifra esadecimale per codificare 4 bit:
- 1112 → 78
- 011 1112 → 378
- Analogamente, poiché 8 = 23 è possibile utilizzare una cifra ottale per codificare 3 bit:
- 1010 11112 → AF16
- 1111 11112 → FF16
1.3.1. Rappresentazione dei registri
Un computer le grandezze numeriche sono elaborate mediante sequenze di simboli di lunghezza fissa dette parole, poiché una cifra esadecimale codifica 4 bit:
- 1 byte (8 bit) → 2 cifre esadecimali
- 2 byte (16 bit) → 4 cifre esadecimali
- 4 byte (32 bit) → 8 cifre esadecimali
- 8 byte (64 bit) → 16 cifre esadecimali
1.3.2. Numeri con parole di lunghezza fissa
I registri dei computer moderni sono tipicamente a 32 o 64 bit. Con parole di lunghezza fissa sono rappresentabili un nmero finito di naturali. Con m bit di lunghezza possiamo rappresentare 2m-1 naturali. Siccome le parole sono di lunghezza fissa, anche per un numero che richiede meno cifre dovremo utilizzare degli zeri di riempimento. Esempio di rappresentazione del numero 4 in biario con parole di 8 bit: \[00000100_2\].
Quando un'operazione produce un numero troppo grande per essere rappresentato dalla parola a causa della dimensione fissa avviene il fenomeno dell'overflow.
1.4. Rappresentazione dei numeri interi
1.4.1. Con segno
Nella rappresentazione con segno il bit più significativo rappresenta il segno del numero. Per questo motivo con questa codifica sarà possibile, con m bit, rappresentare i numeri da -(bm-1-1) a bm-1.
Bisogna prestare attenzione delle operazioni di somma e sottrazione: dovremo infatti mantenere il segno del numero maggiore in termini di valore assoluto.
1.4.2. Complemento a due
La rappresentazione è analoga a quella con segno, con la differenza che il bit più significativo non rappresenta il segno, ma direttamete il massimo numero negativo rappresentabile (-2m-1):
| Numero binario | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| Valore | -128 | +0 | +0 | +16 | +8 | +4 | +0 | +0 |
Lo zero ha un'unica rappresentazione e il range di rappresentazione è [-2m-1,2m-1-1]. Per complementare un numero dobbiamo invertirne le cifre e aggiungere 1:
- 2 = 0010 → -2 = 1101 + 0001 = 1110
L'overflow in complemento a due avviene solo quando gli operandi sono entrambi positivi o negativi e il risultato ha segno opposto. Esempio con 4 bit:
- 0111 + 0111 = 1000
1.4.3. Binary Coded Decimal
La codifica BCD è una codifica ridondante utilizzata per fornire una naturale rappresentazioe binaria del sistema decimale. Vengono utilizzati 4 bit ma solo e posizioni da 0 a 9 vengono impiegate. Ogni cifra viene codificata singolarmente e non viene rispettato il sistema posizionale. Esempio:
- Il numero 44 viene rappresentato come 0100 0100BCD → Le singole cifre decimali vengono codificate indipendentemente.
1.5. Numeri con virgola
Per rappresentare un numero con virgola in una generica base b: \[ \sum_{i=-k}^{h-1} s_i \cdot b^i \] Dove:
- n è il numero di cifre presenti;
- si è la i-esima cifra;
- bi è la base elevata alla i-esima posizione;
- −k è l’indice dell’ultima cifra dopo la virgola
Esempio in base dieci con il numero 10,46:
- 1 × 101 + 0 × 100 + 4 × 10-1 + 6 × 10-2
1.5.1. Cambiamenti di base con virgola
Si procede separatamente a convertire la parte intera e la parte reale nel caso di conversione da una base a ad una base b di un numero n con virgola:
- Per la parte intera si procede come per i numeri interi
- Per la parte frazioaria il procedimento è inverso:
- Si moltiplica n per b
- La parte frazioaria del risultato si moltiplica ancora per b e la uova parte intera costituisce la seconda cira frazionaria
- Si riparte dallo step 1 fino a quando la parte frazionaria non è 0 o si è raggiunta la precisione desiderata
Esempio di coversione del numero 3,2 da base 10 a base 7:
- Parte intera: 310 → 37
- Parte frazionaria:
- Primo passaggio: \(0,2 \times 7 = 1,4\) ⇒ \(1\) è la prima cifra della parte frazionaria in base 7.
- Secondo passaggio: \(0,4 \times 7 = 2,8\) ⇒ \(2\) è la seconda cifra della parte frazionaria in base 7.
- Terzo passaggio: \(0,8 \times 7 = 5,6\) ⇒ \(5\) è la terza cifra della parte frazionaria in base 7.
La rappresentazione del numero \(3,2_{10}\) in base 7 è quindi: \(3,125_7\).
1.5.2. Virgola fissa
Nella rappresentazione dei numeri con virgola fissa, utilizziamo parole con lunghezza fissata di \(m\) bit per rappresentare i numeri. Questo comporta notevoli svantaggi dal momento che gli \(m\) bit vengono divisi in due sotto-parole:
- I primi \(h\) bit (\(h
- I restanti \(k = m-h\) rappresentano la parte frazionaria
1.5.3. Virgola mobile
Fissare a priori la lunghezza della parte intera e di quella frazionaria costituisce una scelta rigida. Per ovviare a queste difficoltà è stata introdotta la rappresentazione a virgola mobile. Questo tipo di rappresentazione permette di rappresentare un numero reale con una tripla \((s, e, m)\), dove:
- \(s\) determina il segno: \(0\) per positivo, \(1\) per negativo;
- \(e\) è detto esponente;
- \(m\) è detta mantissa e viene rappresentata in notazione scientifica come \(1.xyz\), normalizzata.
La rappresentazione completa di un numero reale è: \[ x = (-1)^s \times m \times b^e \]
Si utilizza sempre la rappresentazione scientifica in cui \(1 \leq m < b\), perché esistono infiniti modi di rappresentare un numero reale \(x\). Ad esempio, per \(3.46_{10}\):
- \(0.356 \times 10^1\)
- \(0.0356 \times 10^2\)
- \(34.6 \times 10^{-1}\)
1.5.4. Standard IEEE 754
L'IEEE 754 è lo standard per la rappresentazione dei numeri a virgola mobile. I numeri possono essere rappresentati con precisione singola (32 bit) o doppia (64 bit):
| Precisione | Segno | Esponente | Mantissa |
|---|---|---|---|
| Precisione singola | 1 bit | 8 bit | 23 bit |
| Precisione doppia | 1 bit | 11 bit | 52 bit |
Per la codifica dell’esponente si utilizza la rappresentazione polarizzata (\(e = e' + P\)), dove: \[ P = 2^{k-1} - 1 \] Avendo 8 bit (\(k = 8\)): \(P = 2^7 - 1 = 127\). In altre parole, gli esponenti sono codificati in ordine crescente.
1.5.5. Esempio di Codifica IEEE 754
Per convertire il numero \(-4.63\) in binario:
- Segno: \(1_2\) (Il numero è negativo).
- Parte intera in binario: \(4 \to 100_2\).
- Parte frazionaria in binario:
- \(0.63 \times 2 = 1.26 \to 1\)
- \(0.26 \times 2 = 0.52 \to 0\)
- \(0.52 \times 2 = 1.04 \to 1\)
- \(0.04 \times 2 = 0.08 \to 0\)
- Risultato: \(0.101_2\).
- Unione della parte intera e frazionaria: \(100.0101_2\).
- Normalizzazione: Spostiamo la virgola di 2 posizioni:\[100.101_2 = 1.000101_2 \times 2^2\]
- Calcolo dell’esponente polarizzato:\[e = 127 + 2 = 129 \to 10000001_2\]
Costruzione del numero a 32 bit:
Segno Esponente Mantissa 1 10000001 00010100000000000000000
1.6. TODO Codifica dei caratteri alfanumerici
I processori moderni non posseggono istruzioni per il trattamento dei caratteri, per questa ragione è necessario codificarli in numeri interi con i quali il calcolatore può lavorare. Un testo è una sequeza di caratteri e i codici associano un numero ad ogni sequenza.
1.6.1. Ascii
Codice a 7 bit: 95 caratteri stampabili e 33 di controllo assegnati ai primi 32 numerali: – null indica la fine di una stringa – carriage return porta il cursore su una nuova riga (andata a capo) – horizontal tab è l’usuale carattere tab
| Decimal | Hex | Binary | Char | Description |
|---|---|---|---|---|
| 0 | 00 | 00000000 | NUL | Null |
| 1 | 01 | 00000001 | SOH | Start of Header |
| 2 | 02 | 00000010 | STX | Start of Text |
| 3 | 03 | 00000011 | ETX | End of Text |
| 4 | 04 | 00000100 | EOT | End of Transmission |
| 5 | 05 | 00000101 | ENQ | Enquiry |
| 6 | 06 | 00000110 | ACK | Acknowledge |
| 7 | 07 | 00000111 | BEL | Bell |
| 8 | 08 | 00001000 | BS | Backspace |
| 9 | 09 | 00001001 | TAB | Horizontal Tab |
| 10 | 0A | 00001010 | LF | Line Feed |
| … | … | … | … | … |
1.6.2. Unicode
Codice a 21 bit (1 milione di simboli). Attualmente (v. 9.0) definiti circa 128.000 caratteri! Viene ulteriormente codificato in UTF-8.
| Codice | Carattere | Significato |
|---|---|---|
| U+0434 | д | Lettera cirillica “de” |
| U+6328 | ب | Lettera araba “ba” |
| U+0E10 | ฐ | Lettera tailandese “tho than” |
| U+1F63A | 😺 | “Smiling cat face with open mouth” |
| U+1F382 | 🎂 | Torta di compleanno |
1.6.3. TODO UTF-8
La codifica UTF-8 è una codifica variabile che usa da 1 a 4 byte per rappresentare ciascun carattere Unicode. La lunghezza della sequenza di byte dipende dal valore del carattere, e il primo byte della sequenza di ogni carattere indica quanto lunga sarà la sequenza complessiva.
La codifica UTF-8 si basa su una sequenza di byte, e il primo byte (il cosiddetto "byte di controllo") definisce la lunghezza della sequenza.
2. Algebra di Boole
- 2.1. Porte Logiche
- 2.2. Funzioni Booleane
- 2.3. Circuiti digitali
- 2.4. Reti Combinatorie
- 2.5. Ricavare tabelle da espressioni
- 2.6. Ricavare espressioni da tabelle
- 2.7. Algebra di Boole
- 2.8. Teoremi di De Morgan
- 2.9. Completezza degli operatori
- 2.10. Schemi circuitali
- 2.11. Mappe di Karnaugh
- 2.12. Display a 7 segmenti
- 2.13. Multiplexer
- 2.14. TODO Decoder
2.1. Porte Logiche
Le porte logiche sono i componenti fondamentali che costituiscono un calcolatore, essere prendono uno o più input e realizzano un output. Gli input si indicano generalmente con le prime lettere dell'alfabeto mentre gli output con le ultime
Porte logiche fondamentali:
AND (Congiunzione):
A B A ∧ B 0 0 0 0 1 0 1 0 0 1 1 1 OR (Disgiunzione):
A B A ∨ B 0 0 0 0 1 1 1 0 1 1 1 1 NOT (Complemento):
A ¬A 0 1 1 0
Altre porte logiche ottenibili combinando le porte fondamentali:
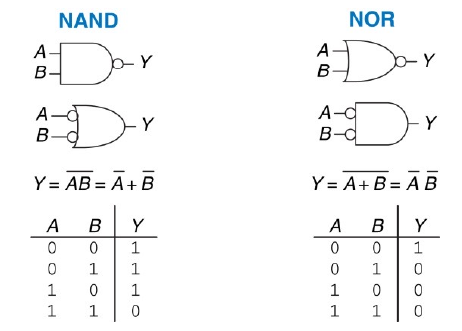
NAND, che si ottiene mettendo in serie una porta AND e una porta NOT:
A B A ↑ B 0 0 1 0 1 1 1 0 1 1 1 0 XOR, che si ottiene mediante la combinazione di porte AND, OR e NOT:
A B A ⊕ B 0 0 0 0 1 1 1 0 1 1 1 0 \[ A \oplus B = (A \land \neg B) \lor (\neg A \land B) \]
XNOR, che equivale alla negazione dello XOR:
A B A ≡ B 0 0 1 0 1 0 1 0 0 1 1 1 \[ A \leftrightarrow B = \neg (A \oplus B) = \neg((A \land \neg B) \lor (\neg A \land B)) \]
- NOR, che equivale alla negazione dell'OR:
A B ¬ (A ∨ B) 0 0 1 0 1 0 1 0 0 1 1 0
Le porte logiche possono avere anche più linee di input, ad esempio possiamo avere una porta AND con quattro linee di input.
Nella realizzazione fisica delle porte logiche i valori in ingresso binari devono corrispondere ad una certa grandezza fisica. La grandezza che reifica i valori 0 e 1 è il potenziale elettrico che genera corrente elettrica all'interno del circuito:
- Il valore logico 0 è rappresentato dal valore di potenziale V0 (GRD)
- Il valore logico 1 è rappresentato da un valore di potenziale VDD ≤ 1,5V
Un circuito è soggetto a rumore che potrebbe alterare i valori nominali, per questo si impiegano delle bande di guardia attraverso delle soglie di tolleranza:
- GRD-VOL
- VOH - VDD
2.2. Funzioni Booleane
\[ f: \{0, 1\}^N \to \{0, 1\} \]
Avendo a disposizione parole di \(N\) bit, abbiamo a disposizione \(2^N\) combinazioni possibili. Essendo che una funzione booleana può assegnare ad ogni combinazione un valore di \(0\) o \(1\), abbiamo quindi \(2^{2^N}\) funzioni booleane possibili:
| x1 | x2 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 | f16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| AND | XOR | OR | NOR | XNOR | NAND |
2.3. Circuiti digitali
Un circuito digitale è una rete che elabora segnali discreti. Prescindendo dalla sua configurazione interna, possiamo vederli come delle black-box con:
- Uno o più input/output
- Una specifica funzionale (relazione fra input e output)
- Una specifica temporale (ritardo della propagazione degli input fino agli output)
Un circuito è composto inoltre da:
- Elementi (altri circuiti)
- Nodi (che interconnettono gli elementi, i nodi possono essere di input, output o interni)
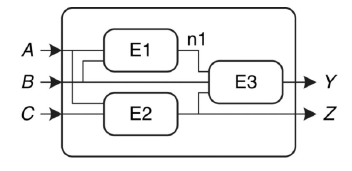
I circuiti digitali si dividono in reti combinatorie e reti sequenziali. In una rete combinatoria il valore degi output dipende esclusivamente dai valori di input correnti, mentre in una rete sequenziale i valori degli output dipendono anche dai valori precedenti (il circuito ha quindi memoria).
2.4. Reti Combinatorie
La composizione di reti combinatorie segue delle regole ben precise:
- Ogni elemento della rete è esso stesso una rete combinatoria
- Ogni elemento non di input connette esattamente un output di un elemento
- Nella rete non devono esistere percorsi ciclici, ogni cammino interno visita un nodo al più una volta
Visualizzare una rete come una scatola nera con un’interfaccia e una funzione ben definite è un’applicazione del principio dell’astrazione e della modularità, così come la costruzione di una rete a partire da elementi circuitali più piccoli è un’applicazione del principio della gerarchia. Le regole della composizione combinatoria sono, infine, un’applicazione della regolarità.
Le specifiche funzionali di un circuito combinatorio sono descritte tramite tabelle di verità o espressioni booleane. Più espressioni booleane corrispondono alla stessa tabella.
2.5. Ricavare tabelle da espressioni
Per ricavare una tabella da un'espressione basta calcolare a ritroso le tabelle delle sue sotto-espressioni: \[ \neg A \land \neg B \oplus \neg (C \land \neg B) \]
| A | B | C | ¬A | ¬B | ¬(C ∧ ¬B) | ¬A ∧ ¬B | Risultato |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
2.6. Ricavare espressioni da tabelle
Per effettuare il procedimento inverso, ovvero ricavare espressioni a partire da tabelle di verità, possiamo servirci delle forme SOP (somma di prodotti) e POS (prodotto di somme). Definizioni preliminari
- Una variabile booleana \(A\) e la sua negata \(\neg A\) sono detti litterali
- Un prodotto di litterali è detto implicante (AND)
- Dato un insieme \(K\) di variabili booleane, un mintermine di \(K\) è un implicante (prodotto ∧) che comprende, positive o negate, tutte le variabili in \(K\).
- Analogamente, un maxtermine di \(K\) è una somma (∨) di litterali che comprende tutte le variabili in \(K\).
- Ordine di precedenza:
- NOT ¬
- AND ∧
- OR ∨
Esempio per \(K = \{A, B, C\}\):
- Mintermine: ¬ A ∧ B ∧ ¬ C
- Maxtermine: ¬ A ∨ ¬ B ∨ C
Se la tabella ha pochi 1 allora la forma SOP è più succinta, altrimenti se ha pochi 0 è meglio utilizzare la forma POS. In caso di numero simile di zero e uno una vale l'altra.
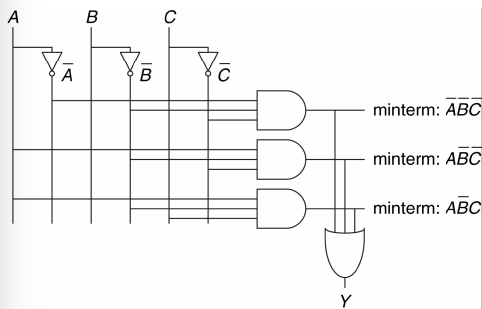
2.6.1. Forma SOP (Sum of Products)
Ognuna delle 2N righe di una tabella di verità è caratterizzata da un mintermine. I mintermini sono enumerati a partire da 0 rigo dopo rigo. Ad ogni tabella di verità corrisponde un'espressione ottenuta sommando tutti i mintermini per cui il valore di output (\(Y\)) della funzione è 1:
| A | B | Y | minterm | minterm name |
| 0 | 0 | 0 | ¬ A ∧ ¬ B | m0 |
| 0 | 1 | 1 | ¬ A ∧ B | m1 |
| 1 | 0 | 0 | A ∧ ¬ B | m2 |
| 1 | 1 | 1 | A ∧ B | m3 |
\[ Y = \sum(m_1, m_3) \] \[ Y = (\neg A \land B) \lor (A \land B) \]
2.6.2. Forma POS (Product of Sums)
La forma POS è la forma duale della SOP e funziona in maniera analoga. Ad ogni riga di una tabella di verità corrisponde un maxtermine che è uguale a 0 solo per quella riga.
| A | B | Y | maxtern | maxterm name |
| 0 | 0 | 0 | A ∨ B | M0 |
| 0 | 1 | 1 | A ∨ ¬ B | M1 |
| 1 | 0 | 0 | ¬ A ∨ B | M2 |
| 1 | 1 | 1 | ¬ A ∨ ¬ B | M3 |
\[ Y = \prod(m_0, m_2) \] \[ Y = (A \lor B) \land (\neg A \lor B) \]
2.7. Algebra di Boole
L'algebra booelana prende il nome dal matematico inglese George Bool. L'oggetto di questa algebra non erano le porte logiche ma le leggi del pensiero e della deduzione, difatti si può dare un'iterpretazione puramente logica alle espressioni booelane.
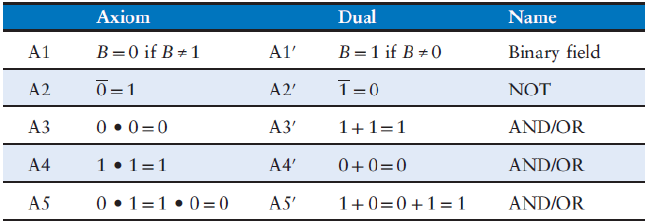
2.7.1. Assiomi dell'algebra di Boole
2.7.2. Teoremi ad una variabile

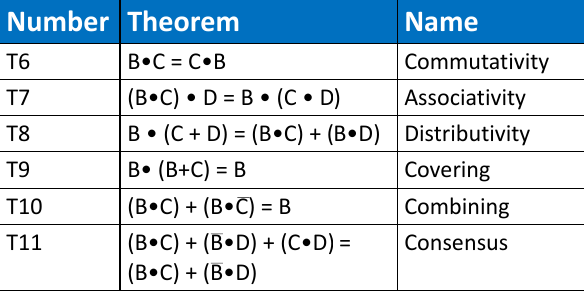
2.7.3. Teoremi a più variabili
2.7.4. Tecniche di dimostrazione
Ci sono diversi modi per verificare se due espressioni booleane sono equivalenti:
- Tramite confronto delle tabelle di verità (Perfect Induction): Questa tecnica è semplice ma priva di intelligenza, al crescere delle espressioni diventa sempre più laboriosa e complessa da gestire.
- Utilizzando gli assiomi ed i teoremi sopra descritti
- Sfruttare la struttura delle espressioni e verificare che le tabelle di verità coincidono solo nei casi rilevanti
2.7.5. Alcuni teoremi per semplificare espressioni
- T8 (Distributivity)
\[ B \land (C \lor D) = B \land C \lor B \land D \] \[ B \lor (C \land D) = (B \lor C) \land (B \lor D) \]
- T9' (Covering)
\[ A \lor (A \land P) = A \]
- T10 (Combining)
\[ (P \land (\neg A)) \lor (P \land A) = P \]
- Expansion
\[ P = (P \land (\neg A)) \lor (P \land A) \] \[ A = A \lor (A \land P) \]
- Duplication
\[ A = A \lor A \]
- "Simplification" theorem
\[ (P \land (\neg A)) \lor A = P \lor A \] \[ (P \land A) \lor \neg A = P \lor (\neg A) \]
2.8. Teoremi di De Morgan
Il teorema di De Morgan ci dice che:
- La negata di un prodotto è uguale alla somma delle negate
- La negata di una somma è uguale al prodotto delle negate

I teoremi di De Morgan ci consentono di convertire una porta AND in una OR e viceversa:
Esempio: \[ Y = \neg((A \lor \neg(B \land C)) \land C) \] \[ = \neg(A \lor \neg B \lor \neg D) \lor C \] \[ = \neg A \land \neg(\neg B) \land \neg(\neg D) \lor C \] \[ = \neg A \land B \land C \lor D \]
2.8.1. Da SOP a POS
I teoremi di De Morgan consentono di ricavare la forma POS a partire dalla SOP (e viceversa):
| A | B | Y | ¬ Y | minterm |
| 0 | 0 | 0 | 1 | ¬ A ∧ ¬ B |
| 0 | 1 | 0 | 1 | ¬ A ∧ B |
| 1 | 0 | 1 | 0 | A ∧ ¬ B |
| 1 | 1 | 1 | 0 | A ∧ B |
\[ \neg Y = \neg A \land \neg B \lor \neg A \land B \] \[ \neg(\neg Y) = \neg((\neg A \land \neg B) \lor (\neg A \land B)) = \neg(\neg A \land \neg B) \land \neg(\neg A \land B) = (A \lor B) \land (A \lor \neg B) \]
2.9. Completezza degli operatori
Qualsiasi funzione booleana \(f:\{0,1\}^N \to \{0,1\}\) può essere spressa in forma SOP. La forma SOP usa solo gli operatori AND (∧), OR (∨) e NOT (¬): questo vuol dire che questo insieme di operatori costituisce un insieme completo. Per le leggi di De Morgan:
- A ∧ B = ¬(¬ A ∨ ¬ B) (AND può essere espresso in termini di NOT e OR)
- A ∨ B = ¬(¬ A ∧ ¬ B) (OR può essere espresso in termini di NOT e AND)
Quindi {NOT, AND, OR} è un insieme di operatori completo ma non minimale, quindi anche {NOT, AND} e {NOT, OR} sono completi.
2.9.1. Operatori insiemistici
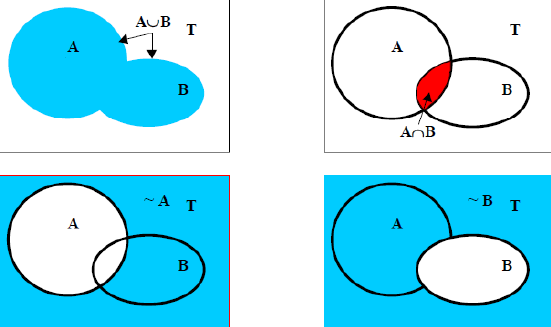
- \( T \): insieme universo
- \( 2^T = \{ A \mid A \subseteq T \} \): insieme dei sottoinsiemi di \( T \)
- \( \cap \): AND
- \( \cup \): OR
- \( T' \): NOT
- \( 1 \): \( T \)
- \( 0 \): \( \emptyset \)
2.10. Schemi circuitali
Uno schema circuitale è un diagramma di una rte digitale che ne mostra gli elementi e i fili che li connettono tra loro. Ad ogni espressione booleane corrisponde un circuito combinatorio. Linee guida da seguire durante la realizzazione di uno schema:
- Gli ingressi vengono collocati in alto o a sinistra
- Le uscite vengono collocate in basso o a destra
- Quando possibile, le porte logiche vanno disegnate in modo che gli ingressi vadano da sinistra verso destra
- I fili dritti si prefeiscono a quelli con troppi angoli
- Fili che arrivano ad una giunzione a T sono collegati
- Un punto disegnato dove due fili si incontrano indica che sono collegati
- Fili che si incrociano ma che non hanno un punto non sono collegati tra loro
Questo stile di disegno è chiamato matrice logica programmabile (PLA) perché i negatori, le porte AND e OR sono allineati in maniera sistematica.
2.10.1. Semplificare formule SOP
Le formule in forma SOP hanno degli schemi circuitali molto regolari:
- Una linea di input per ogni variabile che occorre positiva
- Una linea NOT per ogni variabile che occorre negata
- Una porta AND per ogni mintermine con le linee di input che corrispondono ai relativi litterali
- Tutte le porte AND finiscono in un unica porta OR
La proprietà principale che si utilizza per ridurre le forme SOP è il T10 (Combining): \[ (P \land \neg B) \lor (P \land B) = P \]
Un implicante è detto implicante primo se non può essere combinato con altri implicanti per ottenere un nuovo implicante con meno litterali. Una forma SOP si dice minimale se tutti i suoi implicanti sono primi.
Nella minimizzazione di forme SOP può essere necessario sdoppiare un implicante (T8 ad esempio) allorché questo può essere ridotto in modi differenti.
2.10.2. Semplificare formule POS
Nelle forme POS valgono generalmente le stesse regole delle forme SOP. La proprietà principale che si usa è il combining: \[ (B \lor C) \land (B \lor \neg C) = B \]
2.10.3. Circuito a priorità
I circuiti a priorità vengono utilizzati per assegnare una risorsa condivisa secondo un ordine di priorità fra chi ne fa richiesta.
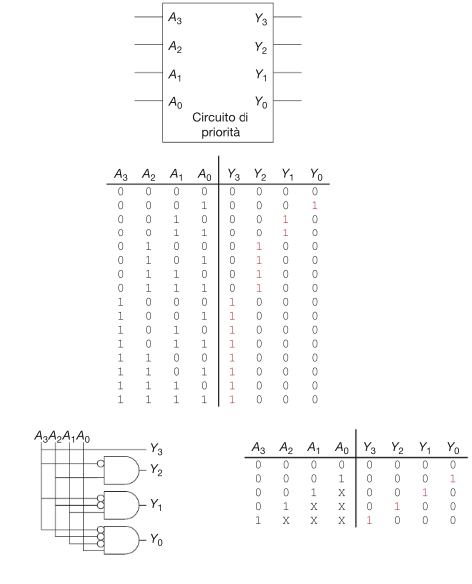
2.10.4. Valori don't cares
Si noti che nel circuito mostrato in precedenza, se A3 è portato a uno, le uscite non tengono conto dei valori degli altri ingressi.
Per progettare un circuito a priorità basta scriverne la tabella di verità, tradurla in espressione e successivamente tradurre l'espressione in porte logiche. Gli ingressi ignorati nelle uscite vengono contrassegnati con una X e vengono chiamati valori Don't cares (o indifferenze).
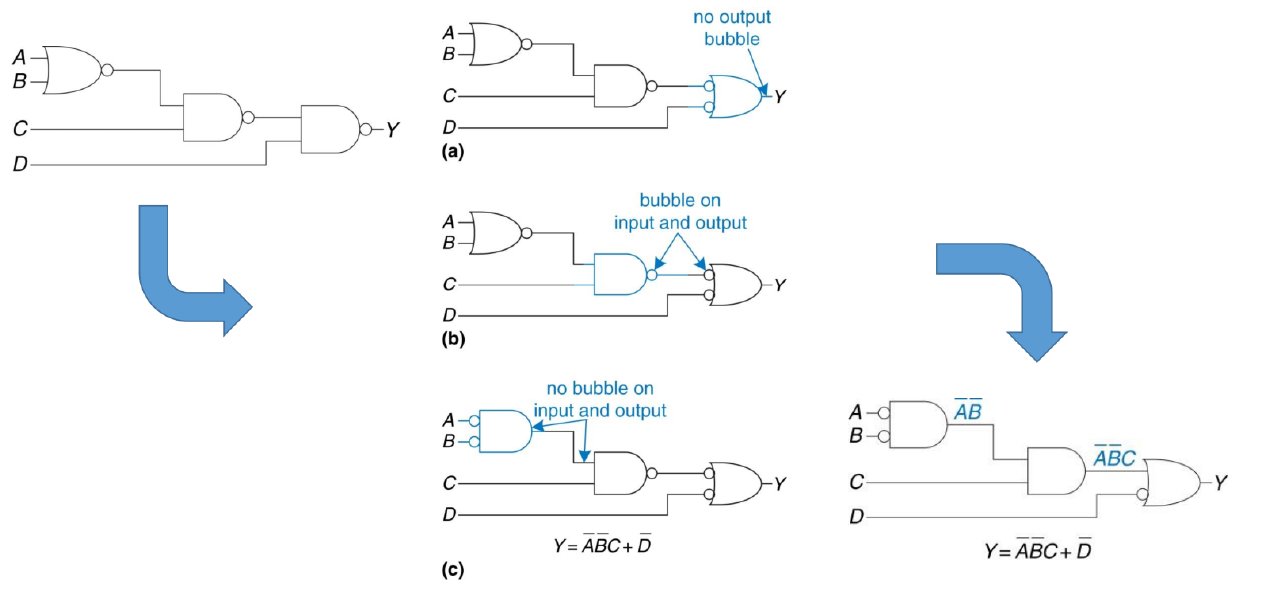
2.10.5. Bubble Pushing
Il bubble pushing è una tecnica grafica che applica le leggi di De Morgan e la legge della doppia negazione per eliminare le negazioni annidate nei circuiti con tante porte NAND e NOR, per semplificarli e renderli più leggibili.
Usare logiche multilivello e porte NAND/NOR a volte rende difficile capire quale funzione booleana un circuito realizza a causa delle molte negazioni annidate. Per avere un'espressione più leggibile si possono applicare le leggi di De Morgan:
- Partendo dall’output Y si applicano a ritroso le leggi di De Morgan in modo che l’input e l’output di ogni nodo siano entrambi positivi o negati
2.10.6. Valori illegali
Si ha un valore illegale quando il valore del potenziale è portato ad essere contemporaneamente sia 0 che VDD, queste configurazioni venono dette illegali perché il valore di Y dipendera dalla natura fisica delle porte:
- Stabile ma indeterminato
- Oscillante fra 0 e VDD
- Possiede un valore intermedio
2.10.7. Alta impedenza e bus condiviso
Un nodo oltre ad essere in uno stato di 0 o 1 può anche trovarsi nello stato \(Z\) di alta impedenza (no passaggio di corrente). Gli stati di alta impedenza vengono utilizzati per disconnettere una parte del circuito dal resto. Per questo si utilizzano i tristate buffer:
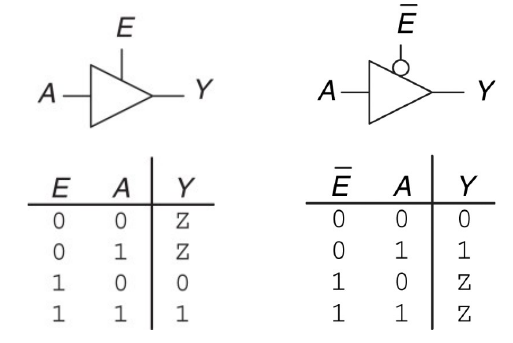
I tristate buffers sono usati in bus che connettono diversi chip per evitare la trasmissione di segnali illegali nel momento in cui più componenti vogliono immetere segnali sul bus, limitando la comunicazione ad un singolo componente per volta.
2.11. Mappe di Karnaugh
Le mappe di Karnaugh sono un metodo grafico per semplificare espressioni in forma SOP.
La proprietà sulla quale si basano le mappe di Karnaugh è il T10 (Combining): \( P \neg B \lor PB = P \)
I numeri binari nella griglia mostrano le combinazioni per tutti i possibili valori di ingresso:
- Dovremmo inserire 1 nelle caselle che, date le opportune configurazioni di ingresso, restituiscono 1 nella tabella di verità dell'espressione
- Successivamente dovremmo raggrupare e cerchiare gli 1 presenti nei riquadri adiacenti
- Per ogni cerchio si deve scrivere l'implicante corrispondente (un implicante è il prodotto tra uno o più litterali)
- Le variabili presenti sia in forma dritta che negata vanno eliminate (vedere la variabile \(C\) nell'esempio)
Regole per il raggruppamento:
- Usare il minimo numero di bolle necessarie per ricoprire tutti gli 1
- Tutte le caselle sottese da una bolla devono contenere 1
- Ogni bolla ricopre un blocco di caselle che è una potenza di 2
- Ogni bolla deve essere più larga possibile
- Dal momento che la mappa ha una struttura toroidale, una bolla può trasbordare la mappa
- Una casella può essere ricoperta da più bolle se così facendo si hanno un numero inferiore di bolle
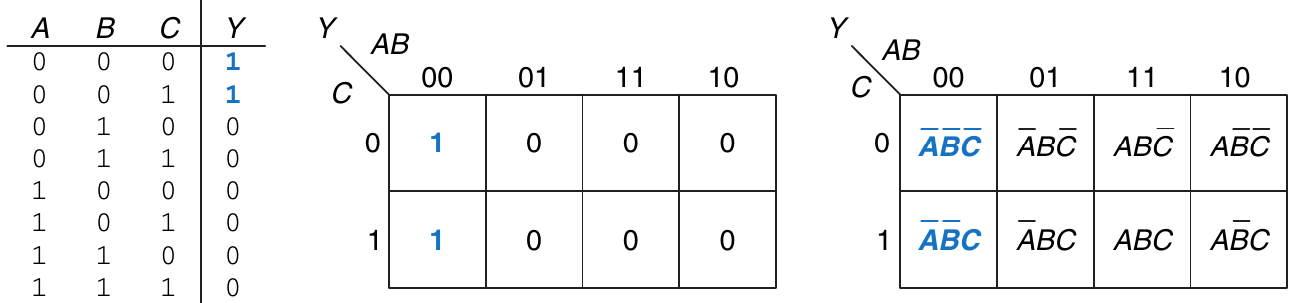
La semplificazione risultante dalla mappa di Karnaugh elimina l'implicante \(C\) (che compare sia in forma dritta che negata) riducendo l'espressione a: \[ \neg A\neg B \]
Risolutore mappe di Karnaugh per controllare la correttezza degli esercizi svolti.
2.12. Display a 7 segmenti
Un decoder display 7 segmenti riceve in input 4 segnali D0:3 e produce sette output Sa:g per controllare i led che rappresentano i numeri da 0 a 9.
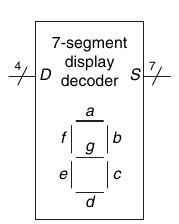
Ogni output è una funzione indipendente a 4 variabili che accende o spegne un singolo segmento del display. Attraverso le tabelle di verità è possibile ricavare le funzioni booleane associate ad ogni segmento.

| D3:0 | Sa | Sb | Sc | Sd | Se | Sf | Sg |
|---|---|---|---|---|---|---|---|
| 0000 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 0001 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0010 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0011 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0100 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0101 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0110 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0111 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1000 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1001 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| others | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
2.12.1. Don't care in output
I valori da 10 a 15 producono sempre lo stesso output (0) dal momento che sono indifferenze. Possiamo sfruttare a nostro vantaggio queste indifferenze e trattare gli output come 0 o 1 a nostra discrezione durante la costruzione delle mappe di Karnaugh.
I valori \(X\) (le indifferenze) possono essere impiegati quando il loro utilizzo ci consente di cerchiare più valori 1 con meno bolle o utilizzando bolle più grandi.
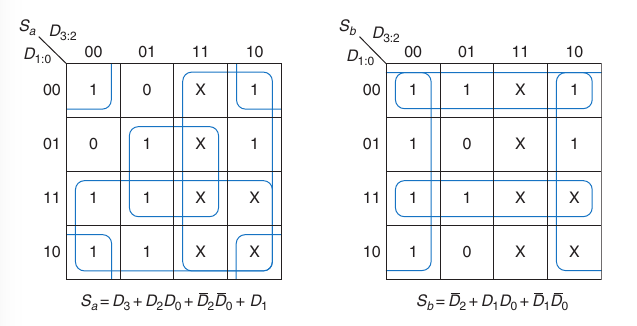
2.13. Multiplexer
I multiplexer (mux) sono tra i circuiti combinatori più utilizzati. I mux selezionano un output da vari input in base al valore di un segnale select.
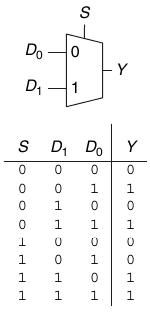
2.13.1. Multiplexer 2:1
Un multiplexer 2:1 riceve in input due segnali D0:1 e un segnale S di selezione. Restituisce in output l'input selezionato dal segnale S. Ad esempio per S = 0, Y = D0 e per S = 1, Y = D1:
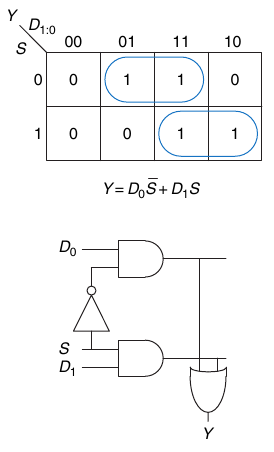
Il circuito di un multiplexer può essere costruito a partire dalla logica SOP:
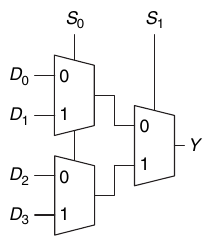
2.13.2. Multiplexer 4:1
I mux 4:1 possono selezionare un segnale da mandare in output partendo da 4 segnali di input D0:3. Per questo motivo servono due segnali di selezione S0:1:
Un multiplexer 4:1 può essere realizzando tramite 3 mutliplexer 2:1:
In generale, per costruire un multiplexer con N ingressi servono log2(N) linee di selezione.
2.13.3. Sintetizzare funzioni booleane con mux
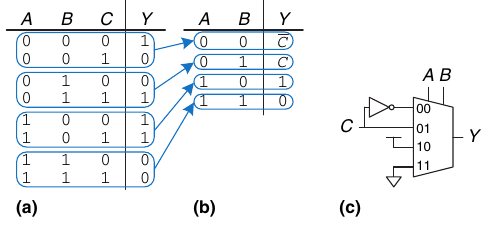
I multiplexer possono essere utilizzati per sintetizzare funzioni booleane. Sintetizzare una unzione di \(m\) variabili con un mux a 2m linee è semplice:
- Le variabili saranno linee di selezione. Data una certa configurazione delle variabii, la linea di ingresso corrispondente sarà posta al valore della funzione in quella configurazione
- Le linee di ingresso riroducono la tabella di verità della funzione
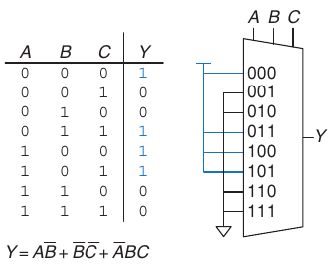
È possibile utilizzare mux con 2m-1 ingressi per sintetizzare funzioni ad m variabili:
- Le prime m-1 variabili saranno linee di selezione
- Le linee di ingresso possono essere poste a 0, 1 oppure all'ultima variabile (positiva o negata)
- Bisogna ridurre la tabella di verità della funzione di partenza
2.14. TODO Decoder
2.14.1. Sintetizzare funzioni booleane con decoder
3. Circuiti sequenziali
I circuiti sequenziali sono dei circuiti le cui uscite dipendono sia dai valori attuali che dai valori precedenti. Di conseguenza, si può dire che i circuiti sequenziali hanno memoria.
3.1. Bistabile
Si definisce circuito bistabile un circuito in grado di tenere due stati stabili. La figura sotto tiportata mostra un semplice circuito bistabile composto da una coppia di NOT connessi a croce. La rete non ha ingressi ma possiede due uscite Q e ¬ Q.
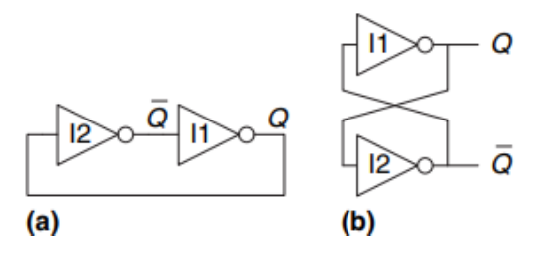
Analisi del circuito:
- Caso 1: \(Q = 0\):
- l2 riceve 0 in input, quindi produce 1 in output.
- l1 riceve 1 in input e produce 0 in output
- Caso 2: \(Q = 1\):
- l2 riceve 1 in input, quindi produce 0 in output
- l1 riceve 0 in input, quindi produce 1 in output
Un circuito con un numero N di stati stabili è caratterizzato da log2N bit di informazione, quindi un circuito bistabile immagazzina un bit di informazione.
Anche se questo circuito è in grado di immagazzinare un bit di informazione, non è molto utile dal momento che l’utente non ha a disposizione un ingresso che permetta di controllare lo stato. Invece altri circuiti bistabili, come ad esempio i latch e i flip-flop, sono provvisti di ingresso per il controllo del valore della variabile di stato.
3.2. Latch
3.2.1. Latch-SR
Il Latch-SR è un circuito sequenziale composto da due porte NOR, collegate a croce. Il Latch-SR ha due ingressi S ed R, e due uscite Q e ¬ Q.
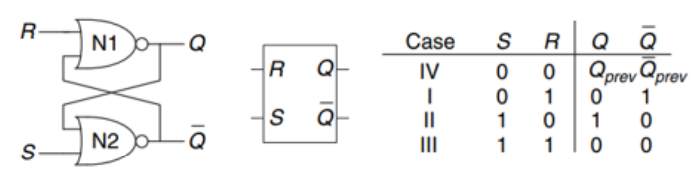
Gli ingressi \(S\) ed \(R\) significano rispettivamente set e reset (da cui il noe Latch Set-Reset). Da notare che la configurazione di partenza \(S = 1\), \(R = 1\) è illegale in quanto otterremo in output \(Q = 0\) e \(\neg Q = 0\), il che è impossibile.
3.2.2. Latch-D
Il Latch-D è un circuito sequenziale che permette di evitate che gli ingressi S ed R del Latch-SR siano simultaneamente attivi. Il Latch-D è composto da due ingressi: un ingresso dati D che controlla in che cosa l'output cambia ed un ingresso CLK, che controlla QUANDO l'output cambia.

3.3. Flip-Flop
3.3.1. Flip-Flop D
Un Flip-Flop D è un circuito sequenziale che può essere costituito da due Latch-D in cascata controllati da due segnali di clock complementari.
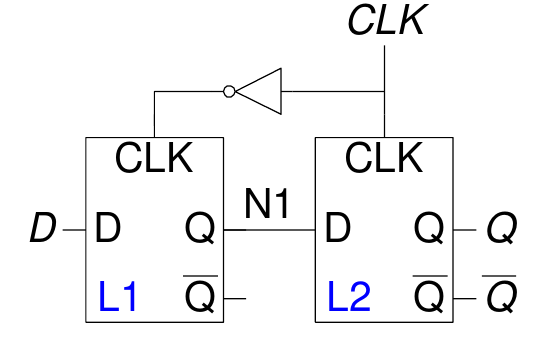
I latch in configurazione Master-Slave (come nel caso del Flip-Flop D) vengono così denominati perché operano in modo complementare, sincronizzati dal segnale di clock (CLK). Di seguito una spiegazione dettagliata del funzionamento:
CLK = 0
Quando il clock è basso:
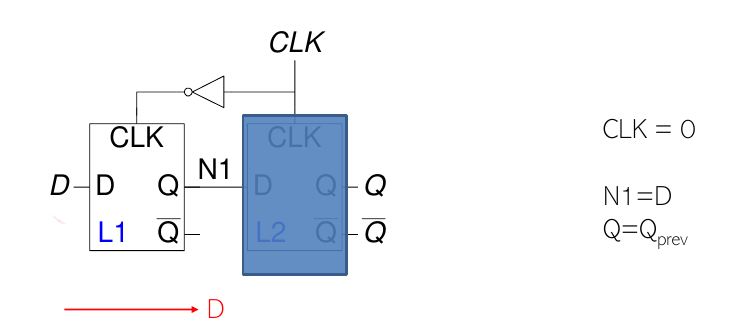
- Il latch master (L1) è trasparente.
- Il latch slave (L2) è opaco.
- Il segnale di ingresso D viene propagato al nodo intermedio N1.
Transizione sul fronte di salita (CLK: 0 → 1)
Durante il fronte di salita del clock:
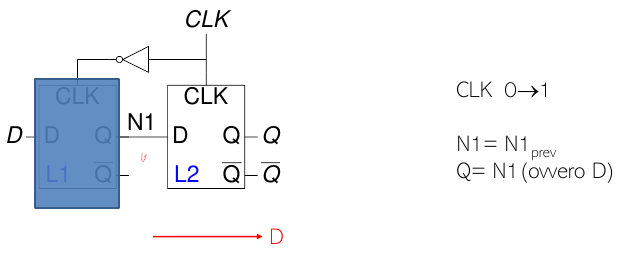
- Il latch master (L1) diventa opaco.
- Il latch slave (L2) diventa trasparente.
- Il dato presente in N1 viene trasferito all'uscita Q.
CLK = 1
Quando il clock è alto:
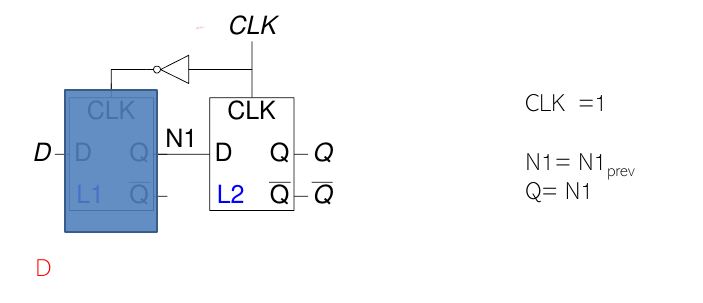
- Il latch master rimane opaco.
- Il latch slave è trasparente, mantenendo stabile il dato sull'uscita Q.
Transizione sul fronte di discesa (CLK: 1 → 0)
Durante il fronte di discesa del clock:
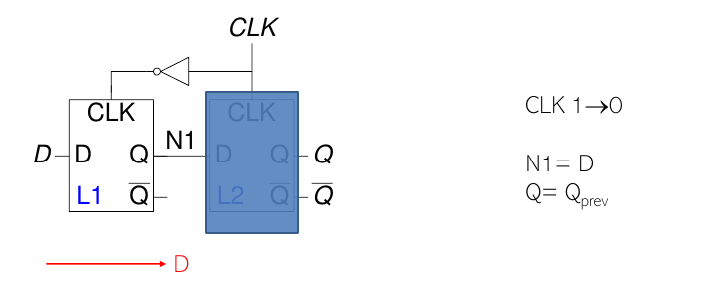
- Il latch master torna trasparente.
- Il latch slave diventa opaco, mantenendo il dato catturato.
Differenze tra Latch-D e Flip-Flop D
- Nei Latch-D, il dato D viene trasferito all'uscita Q quando il latch è trasparente. Il dato può cambiare anche se D varia durante il periodo di trasparenza.
- Nei Flip-Flop D, il dato D viene catturato solo durante il fronte del clock (di salita o di discesa, a seconda della configurazione). Una volta catturato, il dato rimane stabile sull'uscita Q fino al prossimo fronte del clock.
Un cambiamento nel valore di D non avrà effetto sull'uscita Q finché non si verifica il prossimo fronte del clock.
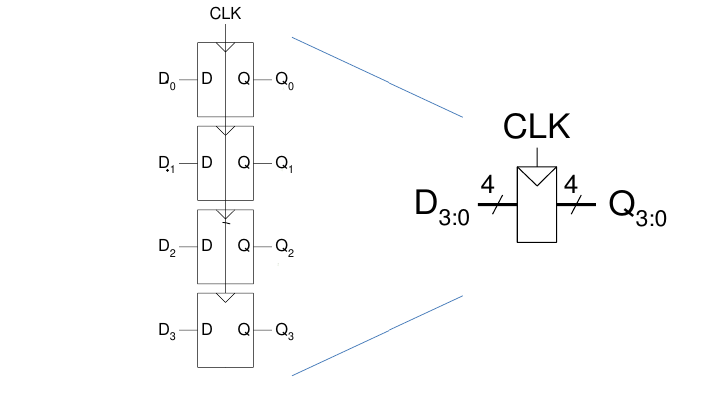
3.3.2. Registri: Multi-bit Flip-Flop
Un registro ad N bit è un banco di N Flip-Flop che condividono un ingresso CLCK comune
Gli input D3:0 e gli output Q3:0 sono bus a 4 bit.
3.3.3. Flip-Flop Enable
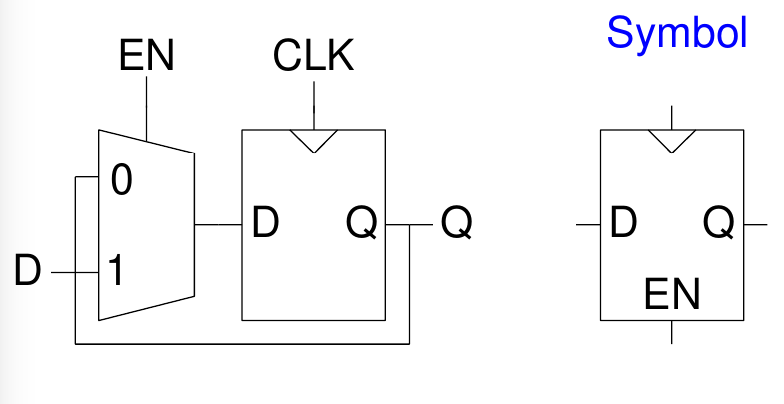
Un Flip-Flop Enable presenta un altro ingresso EN (ENABLE) per determinare se memorizzare o no il dato sul fronte di salita del clock.
- \(EN = 0\): Il Flip-Flop ignora il clock e mantiene il proprio stato (\(D\) passa fino a \(Q\))
- \(EN = 1\): Il Flip-Flop si comporta come un normale Flip-Flop D
3.3.4. Flip-Flop Settabile e Resettabile
Un Flip-Flop resettabile aggiunge un ingresso RESET che, quando è vero, ignora l'ingresso D e porta l'uscita Q a 0.
Questi Flip-Flop possono essere resettati in modo sincrono o asincrono:
- Sincrono: si resettano solo sul fronte di salita del CLK quando RESET = 1
- Asincrono: si resettano non appena RESET = 1
- Per i Flip-Flop asincroni occorre modificare il circuito interno del Flip-Flop
Mentre un Flip-Flop settabile lavora praticamente allo stesso modo:
- Quando SET = 1, allora Q = 1
- Quando SET = 0, il circuito si comporta come un normale Flip-Flop D
3.4. Logiche sequenziali sincrone
I circuiti asincroni presentano delle criticità a volte difficilmente analizzabili che possono dipendere da:
- Struttura fisica dei componenti
- Differenze nella manifattura
- Temperatura
- Tensione in ingresso
Il comportamento di una rete asincrona può quindi variare considerevolmente in base ai ritardi accumulati sui cammini, dato che nei circuiti asincroni l'output è retroazionato in maniera diretta. Per questo motivo si cerca di evitare la retroazione dell'output in maniera diretta e si interpone un registro nel ciclo di retroazione.
Nell’ipotesi che il clock sia più lento del ritardo accumulato sul cammino, il registro consente al sistema di essere sincronizzato col clock: circuito sincrono.
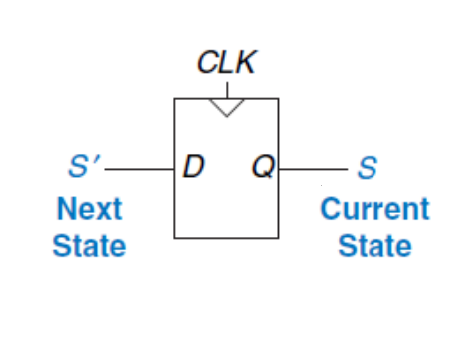
In generale, in una rete combinatoria l'output dipende esclusivamente dall'input: \[ out = f(in) \] Un circuito sequenziale sincrono possiede una serie di stati (\(\{S_0, S_1, ..., S_{k-1}\}\)), quindi l'output dipende sia dai valori attuali che dallo stato corrente: \[ out = f(in, s_c) s_n = g(in, s_c) \]
Per avere una rete sequenziale sincrona, i componenti del circuito devono essere interconnessi in modo che:
- Ogni elemento della rete è o un registro o una rete combinatoria
- Ci deve essere almeno un registro
- Tutti i registri ricevono lo stesso segnale di clock
- Ogni ciclo contiene almeno un registro
L'esempio più comune di rete sequenziale sincrona dato che possiede due stati {0, 1}, dove Q = Sc (current state) mentre D = Sn (next state):
3.5. Macchine a stati finiti (FSM)
3.5.1. Moore FSM
3.5.2. Meeley FSM
3.6.
4. Circuiti aritmetici e memorie
5. ARM assembly
L'architettura di un calcolatore definisce come esso viene visto dal programmatore. Tale architettura è definita in termini di set di istruzioni (linguaggio) e di locazione degli operandi (registri e memoria).
Le parole che costituiscono il linguaggio di un'architettura sono chiamate istruzioni, e il vocabolario delle possibili parole è l'instruction-set del calcolatore. Le istruzioni indicano:
- L'operazione da eseguire
- Gli operandi da usare, che si possono trovare in memoria, nei reistri o nelle istruzioni stesse
Bisogna precisare che l'architettura del calcolatore non definisce la sottostante struttura circuitale, che viene invece definita dalla microarchitettura.
L'architettura ARM rappresenta ogni istruzione con una parola di 32 bit e si basa su 4 principi fondamentali:
- La regolarità favorisce la semplicità
- Rendere veloci le cose frequenti
- Più piccolo è più veloce
- Un buon progetto richiede buoni compromessi
5.1. Operandi: registri, memoria e costanti
5.1.1. Registri
ARM ha 16 registri a 32 bit (R0… R15) fisicamente equivalenti tra loro ma logicamente utilizzati con scopi specifici
| Name | Use |
|---|---|
| R0 | Argument / return value / temporary variable |
| R1-R3 | Argument / temporary variables |
| R4-R11 | Saved variables |
| R12 | Temporary variable |
| R13 (SP) | Stack Pointer |
| R14 (LR) | Link Register |
| R15 (PC) | Program Counter |
5.1.2. Costanti/Immediati
Le costanti si possono definire attraverso l'istrusione MOV:
; R0 = a, R1 = b mov R0, #23 mov R1, #0x45
//int: 32-bit signed word int a = 23; int b = 0x45;
Le costanti così generate hanno una precisione di massimo 8 bit.
Nota: MOV può anche essere usato per spostare il contenuto di un registro in un altro registro:
mov R7, R9